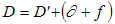Distantele

Instrumente de măsurare directă a distanţelor
Instrumentele utilizate la  măsurarea directă a distanţelor sunt panglicile şi ruletele. Panglica este o bandă de oţel de lungime 20, 25, 30 sau 50 m cu o secţiune de aproximativ 13 * 0.2 mm. Uzual panglicile sunt divizate în metri, decimetri şi centimetri, primul metru având şi diviziuni milimetrice. La un capăt panglica are un inel de prindere, iar celălalt capăt este fixat într-o carcasă sau furcă, prevăzută cu un braţ cu mâner pentru rularea panglicii în carcasă  sau pe cadru. Originea panglicii este de regulă la capătul benzii, la punctul de fixare între inel şi bandă.Ruletele au dimensiuni de 2, 3, 4, 5, 7, 10 sau 20 m şi sunt divizate pe întreaga lungime în m, dm, cm, mm. Secţiunea lor este de regulă mai mică decât cea a panglicilor şi se utilizează la măsurarea distanţelor mici.

Etalonarea şi compararea instrumentelor de măsurare a distanţelor

În mod normal orice instrument de măsurare trebuie verificat şi etalonat înainte de utilizare.Verificarea generală a panlicilor şi ruletelor presupune:

-verificarea aspectului exterior al benzii şi gradul de degradare al diviziunilor;

-verificarea prinderii inelului de întindere de la capătul panglicii;

-verificarea integrităţii panglicii să nu fie ruptă, îndoită, fisurată;

Panglicile şi ruletele au o valoare nominală numai la o anumită temperatură şi forţă de întindere.Pentru instrumentele de oţel temperatura de etalonare este de + 20⁰ C, iar forţa de întindere de 5 kgf respectiv  50 N / l mm² de secţiune de bandă.Etalonarea este procedeul de verificare riguroasă a diviziunilor benzii cu un etalon oficial, stabilind abaterile faţă de valorile nominale înscrise pe bandă.Etalonarea se face în ateliere avizate de Institutul de Metrologie, pe baze speciale de etalonare, stabilind în raport cu originea zero a benzii lungimea reală L_r în dreptul diviziunilor marcate pe bandă. La sfârşitul acestei operaţiuni se întocmeşte un buletin de etalonare a benzii.Compararea benzilor constă în verificarea lungimii întregii benzi fie pe o bază de comparare marcată pe teren orizontal, fie comparând banda cu alta deja etalonată.

Semnificaţia notaţiilor din desen este:

-B – bolţ pentru fixarea panglicii;

-R – scripete pentru greutăţi;

-D – fir de oţel;

-G – greutate;

-M₁ şi M₂ – rigle metalice gradate în mm;

Modul de măsurare a distanţelor pe teren

Măsurarea directă a distanţelor nu necesită explicaţii prea multe deoarece se face pe terenuri cu pantă mică şi pe distanţe relativ mici.În prealabil este necesar ca terenul să fie degajat de obstacole şi jalonat dacă distanţa de măsurat este mai mare decât lungimea panglicii utilizate la măsurătoare.Jalonarea presupune amplasarea de jaloane din 50 în 50 m, începând cu capătul îndepărtat spre cel apropiat de operator.Pentru jalonare sunt necesari doi operatori, unul aşezat pe aliniament, astfel încât să vadă cele două jaloane de la capete ca pe unul singur, iar celălalt operator va planta jaloanele intermediare ghidat fiind de primul.

După jalonare se face măsurarea efectivă a distanţei. La măsurare se vor utiliza ca instrumente auxiliare fişe pentru marcarea capetelor panglicii, întinzătoare şi dinamometre pentru măsurarea forţei de întindere a panglicii.Dacă terenul are variaţii de pantă în lungul aliniamentului de măsurat, acesta se va descompune în segmente de aliniamente cu pantă uniformă, fiecare segment fiind măsurat independent.

Distanţa finală va fi: L = n*l + l^'

-L este distanţa înclinată totală măsurată;

-n este numărul de câte ori a fost aplicată panglica pe teren;

-l este lungimea panglicii;

-l' este distanţa înclinată citită la final de tronson.

Dacă distanţa are pantă se va face reducerea la orizont a distanţei înclinate măsurate pe teren.

D = L sin z = L cosa

-D este distanţa redusă la orizont;

-L este distanţa înclinată măsurată pe teren;

-z este unghiul zenital;

-a este unghiul de pantă;

Corecţia de etalonare

Dacă la măsurare au apărut abateri faţă de valorile nominale ale panglicii acestea trebuie luate în considerare. Corecţia de etalonare se defineşte prin relaţia c_e = l_r - l_n

l_r – lungimea reală rezultată după etalonarea panglicii;

l_n – lungimea nominală înscrisă pe panglică;

Pentru lungimea întregului aliniament măsurat corecţia totală de etalonare este dată de relaţia

C_e = (L_total / l_n )c_e

Lungimea totală corectată este dată de relaţia

L_corectat = L_total + C_e

Se poate determina lungimea corectată şi prin aplicarea unui coeficient de etalonare calculat cu relaţia

k = (l_r / l_n )

Lungimea corectată fiind L_corectat = L_total * k

Corecţia de tensiune sau de întindere

Corecţia datorată variaţiei forţei de întindere faţă de cea de la etalonare se calculează cu relaţia

c_F = ( l_F – l_n ) = [( 1000*ln ) / ( ( S * E )]( F – F₀)

-l_n este lungimea nominală a panglicii;

-l_F este lungimea pangliciiîn timpul măsurătorilor;

-E este modulul de elasticitate al oţelului 2,1 * 10⁴ kg/mm²;

-S este suprafaţa secţiunii transversale a panglicii;

Corecţia totală pentru lungimea măsurată va fi C_F = (L_total / l_n ) * c_F

Lungimea totală corectată este L_corectat = L_total + C_F

Corecţia de temperatură

Funcţie de temperatura din timpul măsurătorilor lungimea benzii va fi l_t = l_e[ 1 + a ( t – t_e )]

-l_t este lungimea panglicii în timpul măsurătorilor;

-l_e este lungimea panglicii la etalonare;

-a este coeficientul de dilatare al oţelului a = 0,0115 mm / 1⁰C / 1m liniar;

-t este temperatura în timpul măsurătorilor;

-t_e este la etalonare;

Corecţia de temperatură pentru o lungime de panglică este 

c_t = Dl_t = l_t – l_e = l_e[1 + a( t – t_e )] - l_e = l_e * a (t – t₀)

Pentru o panglică de oţel de 50 m rezultă corecţia de temperatură

c_t = Dl_t = 50 * 0,0,115 mm (t – t_e) = 0,575 mm ( t – t_e) » 0,6 mm ( t – t_e )

Pentru o lungime oarecare L_total măsurată cu o panglică de 50 m la temperatura t corecţia de temperatură va fi

C_t = 0,6mm ( t – t_e)( L_total / l_e ) 

Semnul corecţiei este dat de semnul diferenţei ( t – t_e ).

Reducerea la orizont a distanţelor

Calculul distanţei reduse la orizont se poate face prin două metode:

-Calculul direct al distanţei orizontale

-Calculul corecţiei de reducere la orizont

Calculul direct al distanţei orizontale

În funcţie de unghiul de pantă a  => D = L * cosa

În funcţie de diferenţa de nivel de la capetele tronsonului Dh => D = ( L² - Dh² )^1/2

Calculul corecţiei de reducere la orizont

În funcţie de unghiul de pantă corecţia va fi 

C_h = DL_h = D – L = L * cosa - L = - L ( 1 - cosa ) = -2 L sin² (a / 2 )

În funcţie de diferenţa de nivel C_h = DL_h = D – L = - [ L – ( L² – h² )^1/2]

Dezvoltând în serie termenul ( L² – h² )^1/2 obţinem corecţia de reducere la orizont 

C_h = - ( h² / 2L ) – ( h⁴ / 8L³ )

Corecţia se aplică cu un termen sau cu doi astfel:

-dacă raportul ( L / h ) > 20, corecţia va fi C_h = - (h² / 2L );

-dacă raportul ( L / h ) < 20, corecţia va fi C_{h =} - ( h² / 2L ) – ( h⁴ / 8L³ );

Distanţa redusă la orizont corectată va fi D = L + C_h

Dacă pe un aliniament sunt variaţii de pantă, acesta va fi descompus în tronsoane de pantă uniformă, tratându-le pe fiecare independent.

Precizia măsurării directe a distanţelor

Erorile care apar la măsurarea directă a distanţelor sunt: erori sistematice şi erori întâmplătoare.

Erorile sistematice sunt:

-eroarea de etalonare;

-eroarea de temperatură;

-eroarea de aliniere;

-eroarea de întindere;

Erorile întâmplătoare sunt:

-eroarea de fixare a originii zero a panglicii;

-eroarea de citire pe panglică ;

Determinarea stadimetrică a distanţelor

Un instrument topografic care are trasate în câmpul vizual al lunetei, atât firele reticulare cât şi firele stadimetrice, va permite determinarea optică a distanţelor.

Considerând cazul particular când axa de vizare a lunetei este perpendiculară pe miră, firele stadimetrice a' şi b', ale lunetei se vor proiecta pe miră în punctele A şi B

Privind prin luneta instrumentului amplasat într-un capăt al distanţei de măsurat, vizând mira amplasată în celălalt capăt, distanţa de determinat, D, este dată de relaţia:

Precizia determinării distanţelor prin acest procedeu este cuprinsă între 0,10m şi 0,20m pentru distanţe de până la 100m.

Determinarea paralactică a distanţelor

Distanţa AB se poate determina şi în condiţiile în care în punctul A este amplasat un teodolit, iar în punctul B, perpendicular pe direcţia AB şi simetric faţă de B, este aşezată mira orizontală MN.

Prin vizarea cu teodolitul a capetelor M şi N, se determină unghiul g  sub care se vede mira.

În triunghiul ABN se poate scrie că:

Dacă b=2m, rezultă că distanţa între A şi B va fi dată de cotangenta unghiului paralactic. Mira astfel construită poartă denumirea de miră BALLA. Teodolitul folosit la astfel de determinări va fi unul de precizie (1^cc....5^cc), iar mărimea unghiului paralactic se va obţine ca medie a mai multor determinări. Pentru a putea obţine determinări precise, latura AB nu va fi mai mare de 60m...80m. 

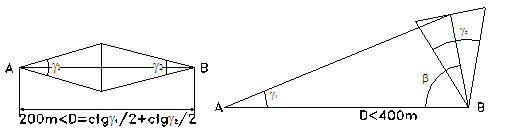
Teodolitul va determina unghiurile paralactice sub care se vede mira din cele două capete ale distanţei.Dacă lungimea este cuprinsă între 200m şi 400 m, atunci la unul din capete se va alege o latură auxiliară, mai mică de 80m, care se va măsura cu mira BALLA. În triunghiul format, se vor măsură toate unghiurile interioare.

Distanţa care dorim să o determinăm va rezulta prin rezolvarea triunghiului.