MĂSURĂTORILE TERESTRE - NOŢIUNI GENERALE
Obiectul şi ramurile măsurătorilor terestre
Topografia face parte dintr-un grup de ştiinţe şi tehnici numite la modul general măsurători terestre, care se ocupă de studiul – determinarea formelor şi dimensiunilor Pământului în ansamblul său, sau pe porţiuni de teren – precum şi de reprezentarea acestora pe hărţi şi planuri.
Măsurătorile terestre au evoluat alături de alte ştiinţe ca: matematica, fizica, astronomia, mecanica cerească şi electronica, care au permis dezvoltarea instrumentelor de măsurare precum şi a metodelor de prelucrare a măsurătorilor.
- Evoluţia ştiinţifică a matematicii a permis dezvoltarea metodelor de prelucrare şi interpretare a rezultatelor măsurătorilor;
- Fizica şi electronica au oferit deschideri noi în domeniul aparaturii utilizate la efectuarea
- Evoluţia ştiinţifică a matematicii a permis dezvoltarea metodelor de prelucrare şi interpretare a rezultatelor măsurătorilor;
- Fizica şi electronica au oferit deschideri noi în domeniul aparaturii utilizate la efectuarea
măsurătorilor.
Măsurătorile terestre au o importanţă deosebită atât în dezvoltarea ştiinţifică cât şi în cea economică.
Măsurătorile terestre au o importanţă deosebită atât în dezvoltarea ştiinţifică cât şi în cea economică.
Ramurile mari ale măsurătorilor terestre sunt:
· geodezia;
· topografia;
· cadastrul;
· fotogrammetria;
Geodezia – este ştiinţa care studiază forma şi dimensiunea Pământului, câmpul gravitaţional în sistem tridimensional, în funcţie de timp. În 1880, Helmert defineşte geodezia ca fiind: „Ştiinţa măsurării şi reprezentării Pământului”. În cadrul acesteia există o serie de subramuri cum ar fi: astronomia geodezică, geodezia marină, geodezia inerţială, geodezia diferenţială.
Topografia – este acea ştiinţă ce se ocupă cu măsurarea şi reprezentarea suprafeţelor relativ mici de teren, fără a ţine seama de curbura Pământului. Denumirea derivă din cuvintele greceşti topos = loc şi grapheim = a descrie. Prin măsurătorile topografice se stabilesc poziţiile relative dintre diverse obiecte din teren şi reprezentarea acestora pe planuri şi hărţi.
Cadastrul – este sistemul unitar şi obligatoriu de evidenţă tehnică, economică şi juridică, prin care se realizează identificarea, înregistrarea, descrierea şi reprezentarea pe hărţi şi planuri cadastrale a tuturor terenurilor, precum şi a celorlalte bunuri imobile de pe întreg teritoriul ţării, indiferent de destinaţia lor şi de proprietar.
Fotogrametria – cuprinde procedee pentru determinarea şi reprezentarea suprafeţelor de teren pe baza unor fotografii speciale numite fotograme obţinute prin fotografierea terenului din avioane echipate adecvat. Caracteristica principală a acestei ramuri este aceea că nu execută măsurători pe teren ci pe imaginea fotografică a acestuia. Fotogrametria nu se aplică independent de alte discipline la întocmirea planurilor şi hărţilor, ci împreună cu topografia, sprijinindu-se amândouă pe reţeaua geodezică.
Suprafeţe terestre
Din punctul de vedere al măsurătorilor terestre, se definesc următoarele trei suprafeţe:
· suprafaţa topografică;
· geoidul;
· elipsoidul.
Suprafaţa topografică – este suprafaţa terenului natural, cu toate caracteristicile lui, aşa cum va fi reprezentat pe hărţi şi planuri. Are forma neregulată şi nu este geometrizată (nu are o formă matematică ce poate fi descrisă prin relaţii matematice).
Geoidul – este o suprafaţă echipotenţială particulară a câmpului gravitaţional terestru, asimilată cu suprafaţa liniştită a mărilor şi oceanelor considerată prelungită pe sub mări şi oceane. Are o formă uşor ondulată, fiind denumită suprafaţa de nivel zero şi constituie originea în măsurarea altitudinilor punctelor de pe suprafaţa topografică a Pământului. Are o formă neregulată şi nu este matematizat. Are proprietatea că în orice punct al său este perpendicular pe verticala VV, respectiv pe direcţia acceleraţiei gravitaţionale, indicată de regulă de firul cu plumb.
Elipsoidul de revoluţie – este suprafaţa geometrică cea mai apropiată de geoid rezultată prin rotirea unei elipse în jurul axei mici 2b, iar axa mică este paralelă cu axa globului terestru.
De-a lungul timpului mai mulţi matematicieni şi geodezi au calculat diverşi elipsoizi în încercarea de-a găsi parametrii optimi.
La ora actuală la noi în ţară se foloseşte elipsoidul Krasovski care are următorii parametri:
a = 6 378 245 m – semiaxa mare
b = 6 356 863 m – semiaxa mică
f =(a-b)/a=1/298,3 - turtirea
Corespondenţa punctelor de pe suprafaţa topografică pe elipsoid se face prin proiectarea punctului aflat pe suprafaţa terestră pe elipsoid prin intermediul normalei NN la elipsoid, iar punctul capătă coordonate geografice.
Coordonatele geografice sunt latitudinea şi longitudinea.
Latitudinea – BP este unghiul format de normala la elipsoid cu planul ecuatorului. Putem vorbi de latitudine nordică sau sudică în funcţie de poziţia punctului într-una din cele două emisfere. Pe ecuator latitudinea este zero.
Longitudinea – LP este unghiul diedru dintre meridianul geodezic ce trece prin punct şi meridianul de origine al elipsoidului de referinţă. Meridianul de origine zero este ales convenţional cel ce trece prin observatorul astronomic de la Greenwich, de lângă Londra.
Sistemul de coordonate geografice are două familii de linii de coordonate:
Lat=const – familia paralelelor
Long=const – familia meridianelor
Pentru România avem:
Latitudinea medie 46oN
Longitudinea medie 25o E Greenwich
Suprafeţe de proiecţie
Prin intermediul sistemelor de proiecţie se face trecerea – prin procedee matematice – de la suprafaţa topografică la suprafaţa plană care este suportul hărţii sau planului topografic. Se ştie că o suprafaţă curbă (gen elipsoid, geoid) nu poate fi transpusă pe plan fără deformarea suprafeţelor sau unghiurilor.
Pentru România sunt adoptate două sisteme de proiecţie:
►Proiecţia stereografică 1970 – STEREO ,70 – cu plan secant unic în centrul geometric al teritoriului, respectiv zona oraşului Făgăraş. Direcţia nord geografic se alfă pe axa X, iar axa Y este paralelă cu direcţia ecuatorului.
►Proiecţia Gauss – proiecţie internaţională, cilindrică, conformă, transversală – aceasta presupune divizarea elipsoidului în 36 de fuse de 6o fiecare. Acestea se desfăşoară de-a lungul meridianului axial, pe un cilindru imaginar.
Elementele topografice ale terenului
Pentru a fi reprezentate pe planuri şi hărţi elementele ce sunt măsurate pe teren, este necesar să descompunem terenul în elemente liniare şi unghiulare măsurabile. Această operaţiune se numeşte geometrizarea terenului şi constă în alegerea punctelor caracteristice de pe teren în aşa fel încât prin unirea lor linia frântă care rezultă să dea cât mai exact forma terenului. Precizia hărţilor şi planurilor depinde de această operaţiune.
Elementele topografice ale terenului în plan vertical
Secţionând terenul în plan vertical vom avea următoarele elemente liniare şi unghiulare:
► aliniamentul AB – o linie sinuoasă, ce urmăreşte linia terenului natural, şi rezultă din intersecţia terenului cu planul vertical;
► distanţa înclinată LAB – este linia dreaptă ce uneşte puntele A şi B;
► distanţa redusă la orizont DAB – este proiecţia în plan orizontal a distanţei înclinate şi este distanţa ce o vom reprezenta pe hărţi şi planuri;
► unghiul de pantă aAB – este unghiul făcut de linia terenului natural cu proiecţia sa în plan orizontal, este un unghi vertical;
► unghiul zenital ZAB – este unghiul făcut de verticala locului cu linia naturală a terenului şi este tot un unghi vertical;
► cotele punctelor A şi B – HA şi HB – sunt distanţele pe verticală de la planul de nivel zero la planurile orizontale ce trec prin punctele A şi B;
Elementele topografice ale terenului în plan orizontal
► unghiul orizontal wAB – este unghiul diedru dintre planele verticale ce trec prin două aliniamente AB şi AC;
► distanţa redusă la orizont DAB – definită mai sus;
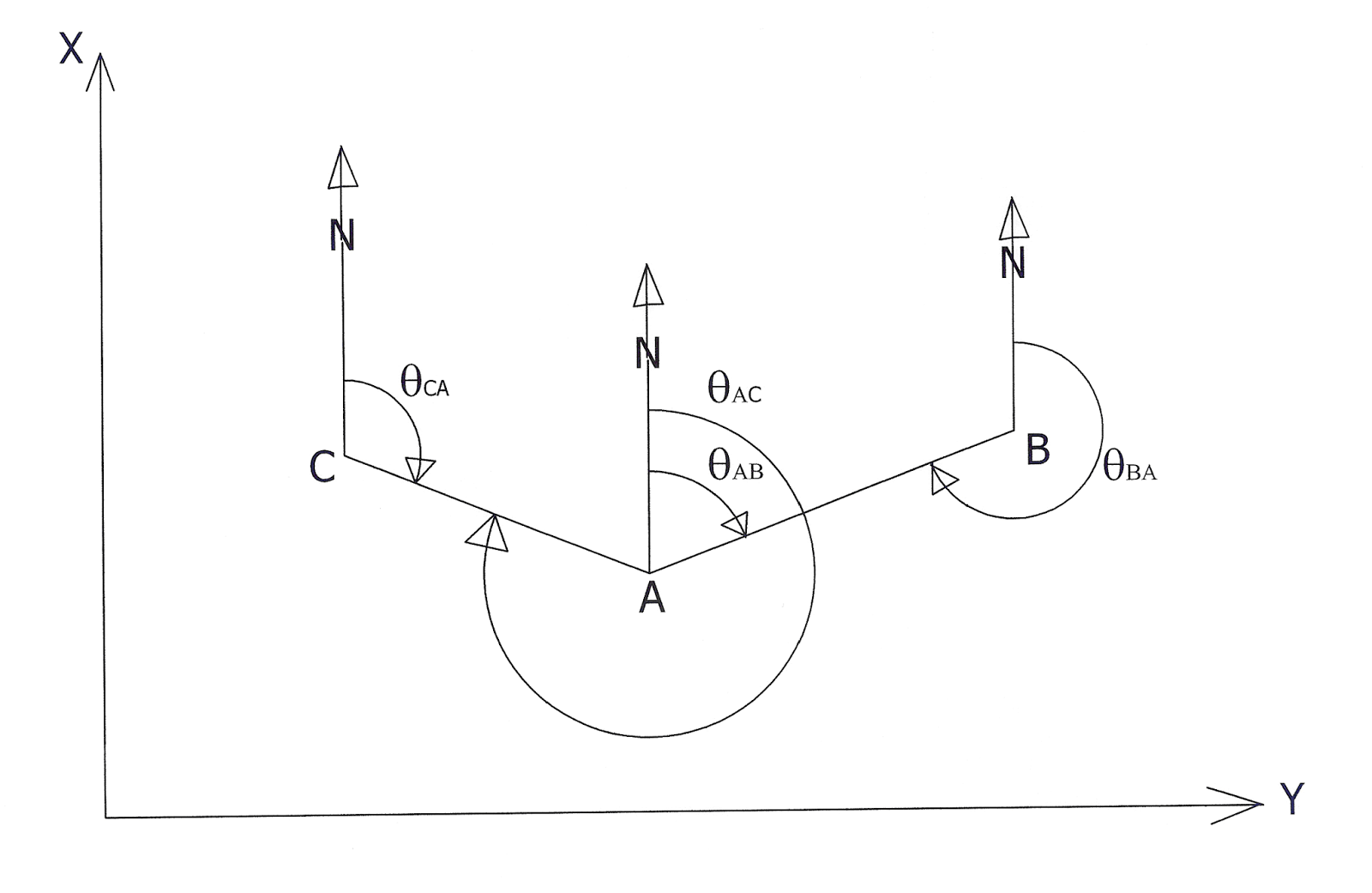
► orientarea topografică qAB – este unghiul orizontal făcut de direcţia nord geografic şi direcţia AB măsurat în sensul acelor de ceas, de la nord spre aliniamentul dat;
În mod convenţional se defineşte orientarea directă qAB şi orientarea inversă qBA. Cele două orientări diferă cu 200g, adică:
qBA = qAB ± 200g
În funcţie de poziţia punctelor în cele patru cadrane vom avea două situaţii:
dacă qAB<200g atunci qBA = qAB + 200g
dacă qAC> 200g atunci qCA = qAC - 200g
Unităţi de măsură
►Pentru lungimi – se foloseşte metrul (m) cu multiplii şi submultiplii săi.
►Pentru suprafeţe – se foloseşte metrul pătrat (m2 ) cu multiplii şi submultiplii. Cel mai uzual multiplu este hectometrul pătrat sau hectarul (ha). 1ha = 10 000 m2.
►Pentru unghiuri – se foloseşte gradaţia centesimală, sexagesimală sau radiani. În topografie în mod uzual se foloseşte gradaţia centesimală.
Trecerea din sistemul sexagesimal în cel centesimal se face prin următoarea corespondenţă:
La cercul de 360o sexagesimale corespund 400g centesimale
1o = 60¢ 1g = 100c
1¢ = 60¢¢ 1c = 100cc
Notaţiile sunt g – pentru grad
c – pentru minute
cc – pentru secunde
Tipuri de coordonate ce definesc punctul şi legătura dintre ele
Un punct pe suprafaţa terestră poate fi definit de trei tipuri de coordonate:
► coordonate geografice BA şi LA – latitudine şi longitudine
► coordonate rectangulare X ,Y,H
► coordonate polare D şi q - distanţa redusă la orizont şi orientarea
Transformarea din coordonate rectangulare în coordonate polare
Dacă avem două puncte 1 şi 2 definite de coordonatele rectangulare X1 şi Y1, respectiv X2 şi Y2 le putem raporta într-un sistem de axe, sistemul STEREO 70 prin raportare carteziană.
Se observă că se formează triunghiul dreptunghic 122¢ în care ipotenuza este distanţa redusă la orizont D12 iar catetele sunt diferenţa de coordonate pe X şi pe Y. Aceste diferenţe se numesc coordonate relative şi se pot exprima astfel:
DX12 = X2 – X1 şi DY12 = Y2 – Y1
Tot aici se poate defini şi unghiul dintre axa X şi distanţa D12 ca fiind orientarea q12 conform definiţiei enunţate la paragraful de mai sus
În concluzie, combinaţia de semne indică cadranul în care se află orientarea fapt pentru care nu se va face un semn din cele două ce rezultă din diferenţele de Y şi X.
Fiecare din cele patru situaţii reprezintă poziţia orientării într-unul din cele patru cadrane ale cercului topografic.
Transformarea din coordonate polare în coordonate rectangulare
Coordonatele relative DX12 si DY12 se pot calcula cu relaţiile:
Astfel coordonata X sau Y a unui punct poate fi calculată funcţie de coordonata altui punct şi coordonata relativă:
X2=X1+D12cosq12
Y2=Y1+D12sinq12
Scara numerică – este raportul constant dintre distanţa ²d² de pe plan dintre două puncte şi distanţa orizontală ²D² dintre aceleaşi două puncte din teren, ambele fiind exprimate în aceleaşi unităţi de măsură.
Scara numerică – este raportul constant dintre distanţa ²d² de pe plan dintre două puncte şi distanţa orizontală ²D² dintre aceleaşi două puncte din teren, ambele fiind exprimate în aceleaşi unităţi de măsură.
Relaţia matematică de exprimare a scării numerice este 1/n=d/D, unde n este numitorul scării, iar d şi D sunt distanţele enunţate mai sus
Valorile scărilor numerice sunt STAS, astfel că putem avea următoarele tipuri de scări:
Precizia grafică a planurilor şi hărţilor
Dacă eroarea de citire sau de raportare a unui punct pe plan sau hartă este de 0.2 – 0.3 mm, valoarea corespunzătoare a acesteia în teren se numeşte precizie grafică. Precizia grafică este direct proporţională cu numitorul scării numerice.
Scara grafică – este reprezentarea grafică a scării numerice. După modul de construcţie al scării grafice, se deosebesc două tipuri: scara grafică liniară cu talon şi scara grafică transversală.
Scara grafică liniară cu talon - se va desena pe planuri şi hărţi printr-o linie divizată, în cm având înscris în dreptul fiecărei diviziuni valoarea distanţei din teren corespunzătoare scării planului. Scara grafică asigură o precizie de 1/10 din bază.
Mod de utilizare: se ia în compas distanţa de pe hartă, dintre două puncte 1 şi 2 şi se aşează compasul pe scară, astfel încât un vârf al compasului să coincidă cu un număr întreg de baze, iar celălalt vârf al compasului să cadă în interiorul talonului. Distanţa este egală cu numărul întreg de baze la care se adaugă partea fracţională citită pe talon.
Exemplu: pentru scara numerică de 1 : 1000 s-a construit scara grafică din figura 1.6. Distanţa măsurată este: 30 m + n*1 m = 30 m + 7*1 m= 37 m
Unde n este numărul de fracţiuni de la zero al scării până la intersecţia cu vârful compasului. Valoarea unei diviziuni este egală cu 1 m.
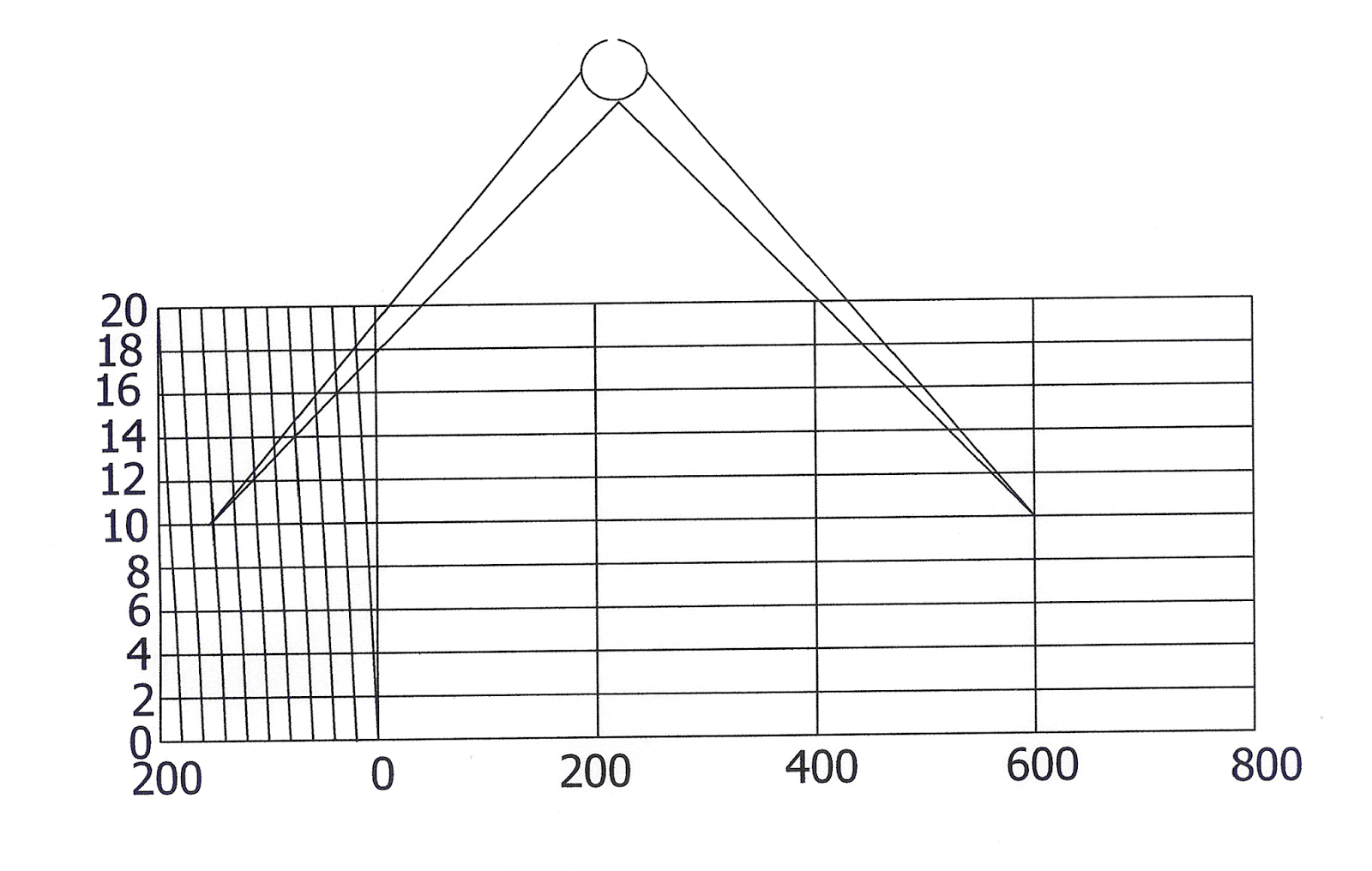
Scara grafică transversală – asigură o precizie de 1/10 din bază, deoarece talonul este împărţit în 10 unităţi pe orizontală şi în 10 părţi pe verticală, astfel că o unitate de pe orizontală reprezintă 1/10 din bază, iar o unitate pe verticală reprezintă 1/10 dintr-o unitate de pe orizontală.
Mod de utilizare: se ia în compas distanţa de pe hartă, între două puncte 1 şi 2 şi se aşează pe scara grafică, astfel încât un vârf al compasului să corespundă cu o diviziune întreagă din bază, iar celălalt vârf să cadă în interiorul talonului scării transversale. Se deplasează compasul astfel ca un vârf să rămână tot timpul pe o valoare întreagă din bază, iar celălalt să fie în talon, până când vârful din talon atinge intersecţia a două linii ce marchează diviziunile lui. Mişcarea compasului se face astfel încât vârfurile lui să fie tot timpul pe aceaşi linie orizontală. Distanţa este egală cu numărul întreg de baze la care se adaugă partea fracţionară citită pe talon.
Mod de utilizare: se ia în compas distanţa de pe hartă, între două puncte 1 şi 2 şi se aşează pe scara grafică, astfel încât un vârf al compasului să corespundă cu o diviziune întreagă din bază, iar celălalt vârf să cadă în interiorul talonului scării transversale. Se deplasează compasul astfel ca un vârf să rămână tot timpul pe o valoare întreagă din bază, iar celălalt să fie în talon, până când vârful din talon atinge intersecţia a două linii ce marchează diviziunile lui. Mişcarea compasului se face astfel încât vârfurile lui să fie tot timpul pe aceaşi linie orizontală. Distanţa este egală cu numărul întreg de baze la care se adaugă partea fracţionară citită pe talon.
Exemplu: pentru scara numerică de 1:10 000 s-a construit scara grafică transversală din figura 1.7. Dacă baza este egală cu 2 cm, distanţa citită cu ajutorul acestei scări este: D12 = 600 m + 150 m = 750 m, unde 600 m corespund numărului de baze întregi iar 150 din citirea pe talon.